지난 번에 엑셀에서 지수평활법 함수를 제공한다고 했는데, 아쉽게도 예전 버전의 엑셀에는 그 함수가 없습니다.
Forecasting techniques (예측기법) 1탄
이번 글에서는 앞서 언급한 forecasting 기법 중 Intrinsic techniques에 대해서 좀 더 자세히 알아보겠습니다. * Average (평균) 과거 데이터의 평균을 구해서 향후 예측을 뿌리는 단순한 방법입니다. 우리
sman7.tistory.com
오늘은 예전 버전의 엑셀을 사용하시는 분들도 사용할 수 있도록 다른 방법을 알려드릴려구요.
바로 해찾기(Solver) 기능인데요.
엑셀에 그냥 있는 건 아니고 별도의 (간단한) 추가 설치 작업이 필요합니다.
엑셀 '해찾기' 기능 추가
파일 → 옵션 → 추가기능 → 해찾기 순서로 들어가셔서 추가기능을 선택해 주시면 아래와 같이 엑셀 리본메뉴에
추가로 생성되는 것을 확인하실 수 있을 겁니다.


참고로, '해찾기' 추가하실 때 '분석도구'도 같이 추가하시면 나중에 통계분석 하실 때 좋습니다.

추가 설치가 끝나셨으면 이 해찾기 기능을 활용하는 방법을 알아보겠습니다.
어떤 회사의 첫번째 기간 실제와 예측치가 다음과 같다고 해보죠.

우리는 지수 평활법을 이용하여 두번째 기간의 예측치를 구할 수 있습니다.
평활상수 (Smoothing constant) α값이 0.1라고 가정했을 때 지수평활법 수식에 대입해 보면,
New forecast = α X latest demand + (1- α) X (previous forecast)
두번째 기간의 예측치는 0.1 X 12 + (1 - 0.1) X 13 이 되어 12.9가 됩니다.

최적의 평활상수 값은 어떻게 찾을까요?
핵심은 과거데이터를 바탕으로 임의의 평활상수를 넣어 예측오차를 구한 다음 그 오차를 최소화하는 평활상수를 엑셀이 역으로 계산하게끔 하는 것입니다.
예를들어, 오른쪽 그림과 같이 과거 14번째 기간까지의 실제값이 있다고 가정해 봅시다.
지수평활법을 활용하여 임의의 평활상수(0.1)를 넣고 14번째 기간까지의 forecasting 값을 입력해 줍니다.
(C7 수식 입력후 아래로 수식복사 해주시면 됩니다)
그리고나서 해당 수식을 14번째 기간까지 적용해 주면 평활상수 0.1을 적용했을때의 예측치가 나오게 되죠.
이제는 이 예측치를 실제 데이터와 비교하여 최대한 갭을 줄일 수 있는 평활상수 값을 찾아주는 작업을 해야 합니다.
Forecasting error를 판단하는 지표 중에 MAD, MAPE 외에 MSE란 것이 있습니다.
Mean Squared Error의 약자로 예측 모델의 성능을 측정하는 데 사용되는 평가 지표 중 하나입니다.
단어의 뜻에서 알 수 있듯이 MSE는 예측값과 실제값의 차이를 제곱한 값의 평균으로 계산됩니다.
MAD가 예측값과 실제값의 차이의 절대값을 평균한 것과 달리 MSE는 차이의 제곱을 평균한 것입니다.
차이점이라고 한다면, 데이터가 통상적인 범위 내에 있지 않고 튀는 숫자들(Outliers)이 많이 있는 경우
MSE로 forecasting 모델의 성능을 측정할 경우 (제곱한 값의 평균이므로) 정확도가 떨어진다고 판단할 수도 있습니다.
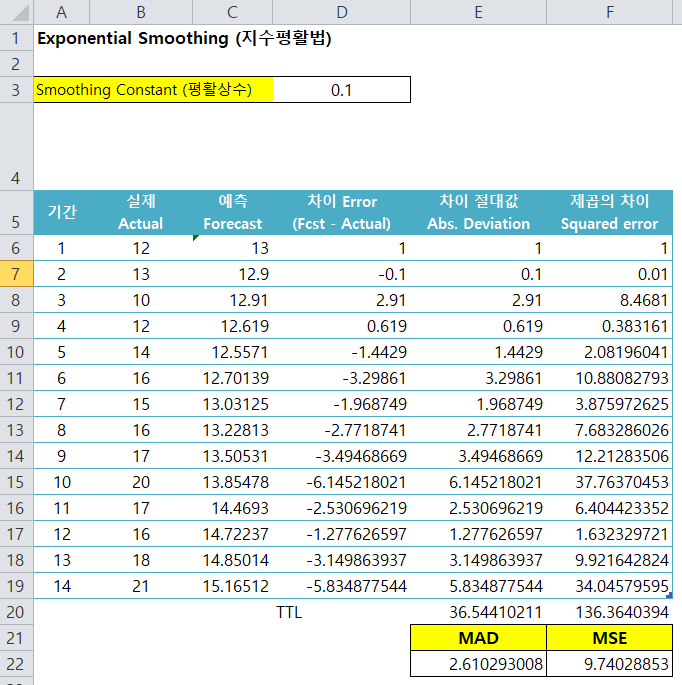
우리가 필요한 데이터는 MAD 혹은 MSE값이므로 좌측의 표와 같이 실제값과 Forecast간의 차, 그 값의 절대값, 그리고 그 값의 제곱을 각각 구해줍니다.
아랫부분에 그 값들의 합(TTL)을 적어주고 해당값의 평균을 구해주면 그 값이 각각 MAD와 MSE값이 되는 것이죠.
최적의 α값이라 함은 forecasting error가 최소인 것으로 생각할 수 있겠죠?
핵심은 MAD, MSE가 최소로 나올 수 있는 값을 엑셀의 해찾기 기능으로 구하는 것입니다.
우리는 현재의 MAD와 MSE값을 최소화 할 수 있는 평활상수가 무엇인지를 찾으면 됩니다.
우선 MAD 를 최소화 할 수 있는 값부터 찾아보겠습니다.
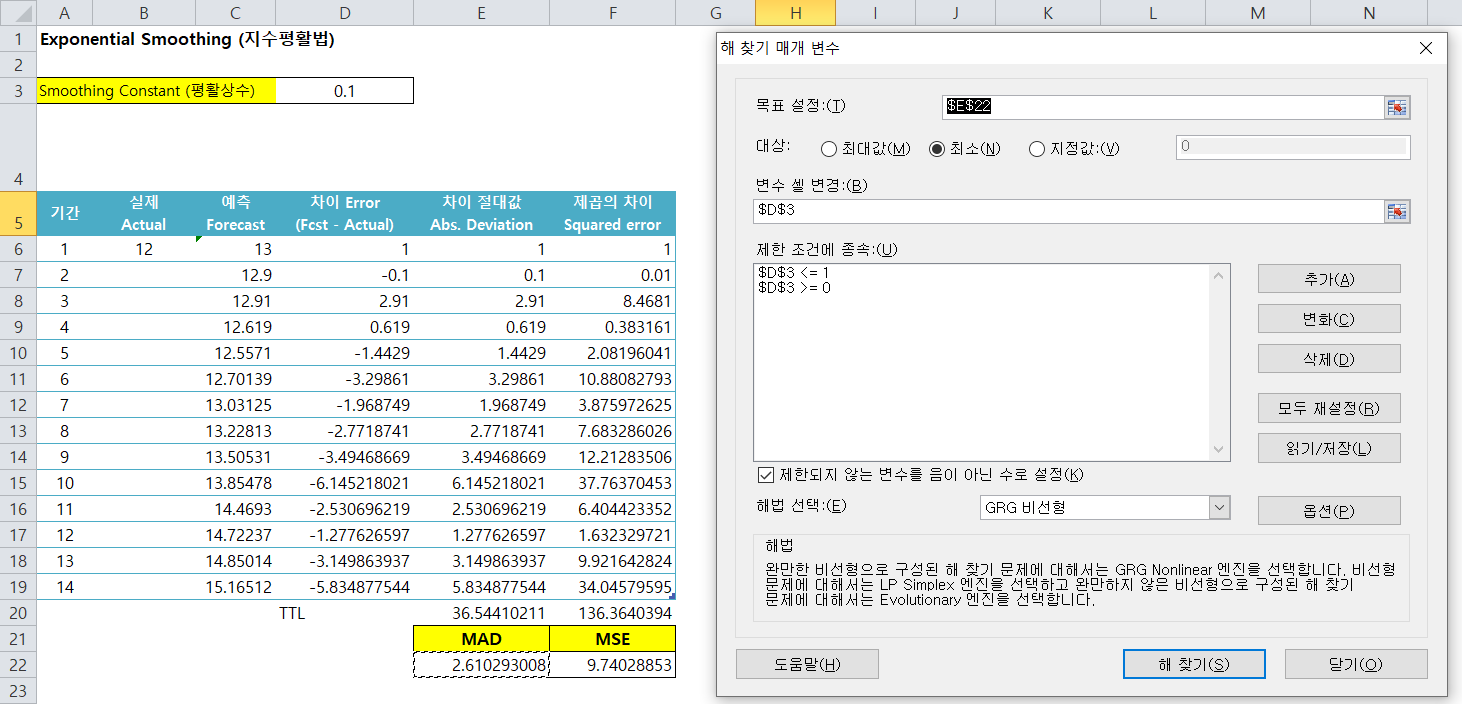
목표는 MAD값의 최소화이므로 '목표설정'값에 MAD 값이 들어있는 셀을 지정, 대상을 '최소'로 해주시구요.
'변수 셀 변경'은 평활상수가 있는 D3값을 지정해 줍니다.
앞선 포스팅에서 평활상수값은 0보다 크고 1보다 작다는 조건이 붙는다고 했었죠?
해당 조건을 '제한 조건'에 추가를 해주신 후 해찾기 버튼을 누르시면 됩니다.
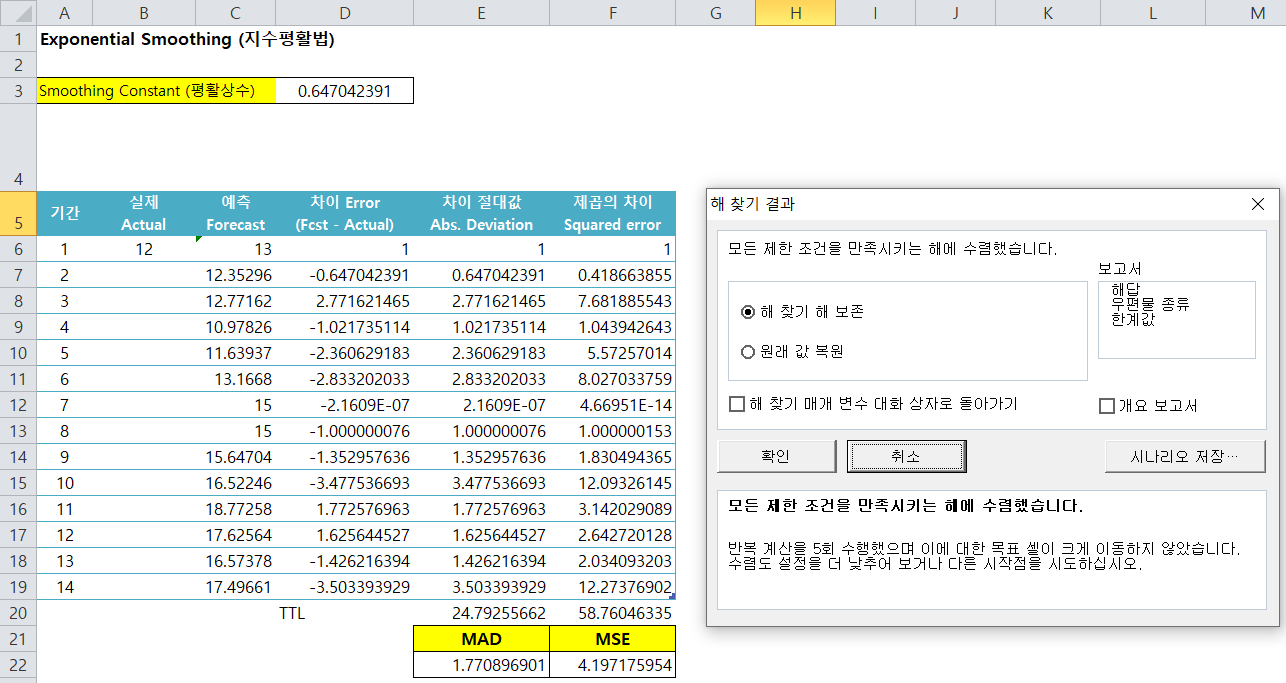
그러면 위와 같이 해찾기가 실행되고 MAD값이 1.77로 떨어지는 평활상수 0.647를 얻으실 수 있는 것입니다.
다음은 MSE값을 최소화하는 평활상수를 구해볼까요?
다른 값은 동일하고 목표설정 지정값을 MSE값으로 바꿔줍니다.
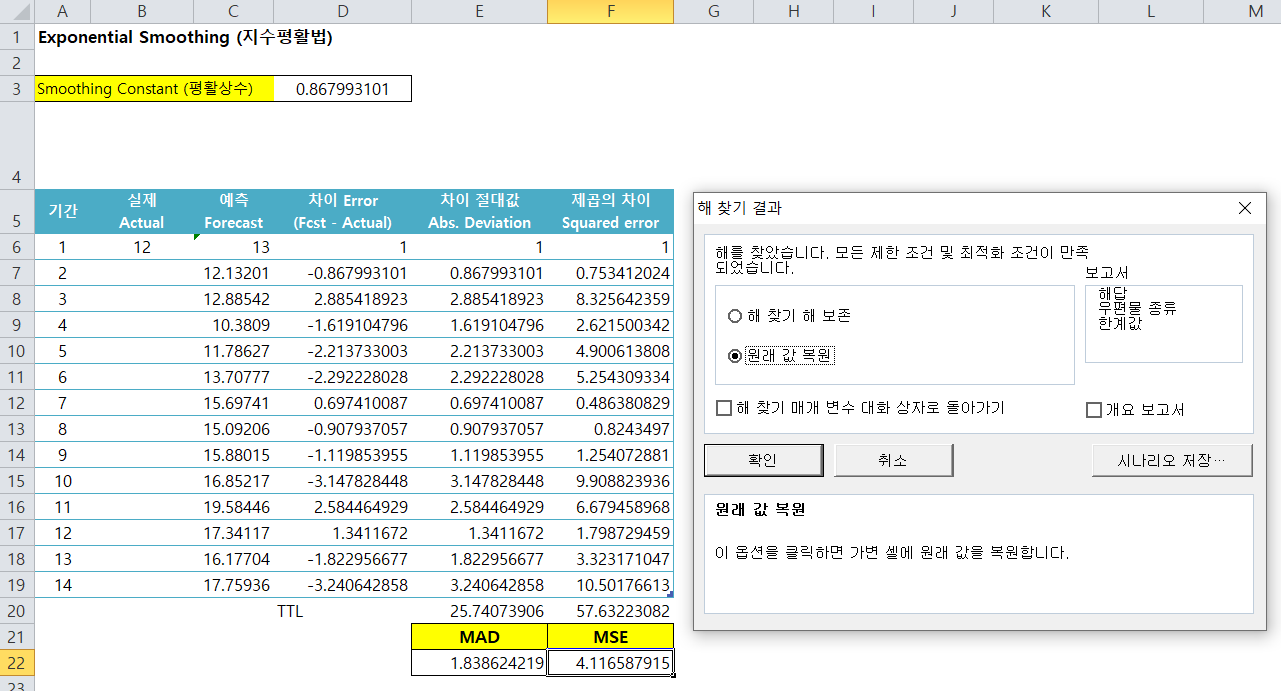
MSE로 할 경우에는 평활상수 값이 0.867이 나왔네요.
MAD든 MSE든 평활상수 값이 0.1 → 0.64, 0.86으로 변경되면서 최근 값을 더 많이 반영하게끔 바뀌게 됨을 알 수 있습니다.
지금까지 언급드렸던 산술평균, 이동평균, 지수평활법 등은
시계열 데이터에서 추세나 계절성의 패턴이 없는(Stationary - 평균을 중심으로 무작위한 변동성을 갖는)
forecasting에 활용할 수 있습니다.
추세(trend) 가 있는 패턴의 경우는 '회기분석'과 'Holt 트렌드 모델'을 사용하는 것이 더 바람직 한데요.
관련해서 계속 업데이트 하도록 하겠습니다.

'SCM' 카테고리의 다른 글
| 선형회귀분석 (Linear regression analysis) - 트렌드를 예측하는 forecasting 모델 (0) | 2023.05.05 |
|---|---|
| MAD (Mean Absolute Deviation)는 무엇이고 MAPE와 다른 점은 무엇일까요? (0) | 2023.05.01 |
| Forecast error의 구분 (0) | 2023.04.28 |
| Forecasting techniques (예측기법) 3탄 (0) | 2023.04.26 |
| Forecasting techniques (예측기법) 2탄 (0) | 2023.04.21 |